Difference between revisions of "User:Jdavis/Forging"
From SpiralKnights
(major edits, more sections) |
(→Advice: remove puffery) |
||
| (7 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | This article explains why | + | This article explains why Spiral Knights should consider forging 5-star items with medium (70%-80%) chances rather than 100% chances. It describes theory and experiment that you can interpret to make the best decision for your level of comfort with risk. |
==Assumptions== | ==Assumptions== | ||
| − | We ignore forge bonuses | + | We ignore forge bonuses entirely. Double level-ups are highly relevant, but they do not appear to be affected by forging chances. Prize boxes are very rare. A 25% heat bonus is not relevant. |
| − | We assume that the tries are independent of one another and that the chances are as stated. Data sets collected by players do not offer any statistically valid evidence that the chances are otherwise. | + | We assume that the forging tries are independent of one another and that the chances are as stated. Data sets collected by players do not offer any statistically valid evidence that the chances are otherwise. |
We also assume that the knight never gives up, no matter how bad her luck is. | We also assume that the knight never gives up, no matter how bad her luck is. | ||
| Line 12: | Line 12: | ||
==Theory== | ==Theory== | ||
| − | When a knight uses 100% forging chances, heating one 5-star item costs | + | When a knight uses 100% forging chances, heating one 5-star item always costs 453 Radiant Fire Crystals. When a knight uses medium chances, the cost of heating a 5-star item varies. |
| − | + | The minimum cost is a mere 302 Radiants. This cost is achieved when all nine forgings from heat level 1 to heat level 10 succeed on their first tries. The probability is | |
| + | :(0.80)<sup>3</sup> * (0.75)<sup>3</sup> * (0.70)<sup>3</sup> = 7.4%. | ||
| + | So 92.6% of the time the cost will be greater than 302. | ||
| − | + | Basic probability theory lets us compute the ''expected cost'', which you can think of as the cost incurred by a knight experiencing average luck. We expect to try 1 / ''p'' times to complete a task, if each trial has probability ''p'' of success. For example, forging from heat level 1 to heat level 2 has ''p'' = 0.80, so we expect 1 / 0.80 = 1.2 forgings and an expected cost of 1.2 * 6 = 7.2 Radiants. | |
| − | + | If we add up the expected costs for all nine forgings, then we find that the expected total cost is around 419 Radiants. That is, '''a knight experiencing average luck will spend 419 Radiants'''. | |
| − | + | ||
| − | If we add up the expected costs for all nine forgings | + | |
Some knights will experience better-than-average luck and spend fewer than 419 Radiants, down to the minimum of 302. Some knights will experience worse-than-average luck and spend more than 419 Radiants. In fact, there is no theoretical maximum. A very unlucky knight might spend more than 1,000 Radiants. | Some knights will experience better-than-average luck and spend fewer than 419 Radiants, down to the minimum of 302. Some knights will experience worse-than-average luck and spend more than 419 Radiants. In fact, there is no theoretical maximum. A very unlucky knight might spend more than 1,000 Radiants. | ||
| Line 26: | Line 26: | ||
==Experiment== | ==Experiment== | ||
| − | To get a more detailed picture of the possible costs, we perform a computer simulation. Working in Python 3.x, we use a random number generator to compute 1,000,000 simulations of knights forging 5-star items from heat level 1 to heat level 10. For each of the 1,000,000 simulations, we record how many Radiants were required. | + | To get a more detailed picture of the possible costs for medium chances, we perform a computer simulation. Working in Python 3.x, we use a random number generator to compute 1,000,000 simulations of knights forging 5-star items from heat level 1 to heat level 10. For each of the 1,000,000 simulations, we record how many Radiants were required. |
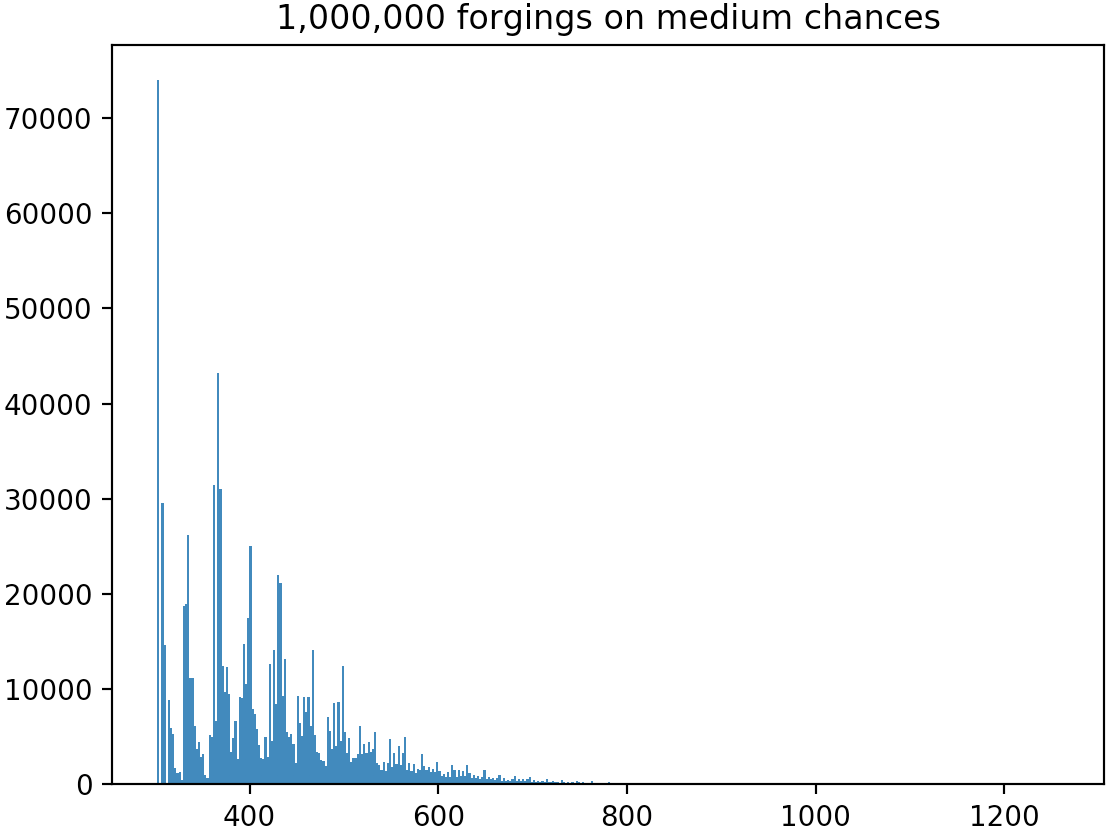
| − | In accordance with the theory, | + | In accordance with the theory, the average is 419.447. The minimum of 302 is achieved in about 7.4% of the simulations. The maximum is 1,258. |
[[File:RadiantsMedium.png|thumb]] | [[File:RadiantsMedium.png|thumb]] | ||
| Line 34: | Line 34: | ||
In the plot, the horizontal axis shows the number of Radiants used, from 302 to 1,258. The vertical axis shows how many of the 1,000,000 simulations used that number of Radiants. | In the plot, the horizontal axis shows the number of Radiants used, from 302 to 1,258. The vertical axis shows how many of the 1,000,000 simulations used that number of Radiants. | ||
| − | + | The median number of Radiants used is 400. The average is greater than the median, because a few simulated knights incurred big costs that pulled up the average. These simulations fill the "long tail" on the right side of the plot. | |
| − | + | For our later analysis, it is useful to identify five "bins" of simulation results. | |
| − | + | * 7% used 302 Radiants. | |
| − | + | * 43% used between 303 and 400. | |
| + | * 20% used between 400 and 452. | ||
| + | * 25% used between 454 and 597. | ||
| + | * 5% used 597 or more. | ||
==Analysis== | ==Analysis== | ||
| − | When forging | + | When forging with medium chances, the only guarantee is that you will spend at least 302 Radiants. You risk spending more than that. But probability theory helps you manage that risk. |
| − | Some knights are highly risk-averse, so they wonder, "How bad could the | + | Some knights are highly risk-averse, so they wonder, "How bad could the cost be?" And the answer is, "There is no limit to how bad it can be." But this attitude is overly pessimistic. A person who is unwilling to accept any risk cannot ride in an automobile, cross a street, walk in a crowd, or do much of anything in life. |
| − | A | + | A reasonable pessimist asks, "How high would the cost be, if my luck were worse than 95% of other knights?" And the answer is around 597. So that kind of knight should forge at 100% chances and accept the 453-Radiant cost. But keep in mind that using 302 Radiants is more probable than using 597 or more. |
A milder pessimist might ask, "How high would the cost be, if my luck were worse than 70% of other knights?" And the answer is around 453. So it makes little difference whether that knight forges at 100% chances or medium chances. | A milder pessimist might ask, "How high would the cost be, if my luck were worse than 70% of other knights?" And the answer is around 453. So it makes little difference whether that knight forges at 100% chances or medium chances. | ||
| − | However, the | + | However, the best assumption is arguably that you will experience average luck. Then forging costs you somewhere around 419 (average) or 400 (median) Radiants. So you should forge with medium chances and save 34-53 Radiants per item. |
| + | |||
| + | The assumption of average luck is especially appropriate for knights who heat many items over a long time period. Even if these knights start off lucky or unlucky, their cumulative luck tends to approach the average as they heat more and more. This phenomenon is called [https://en.wikipedia.org/wiki/Regression_toward_the_mean regression toward the mean]. | ||
| − | + | Knights who are on Cradle for a short time and heat only a few 5-star items are more probable (but still not highly probable) to experience extremes of good or bad luck. For them, adopting a pessimistic attitude to avoid the worst-case scenario makes slightly more sense. | |
==Advice== | ==Advice== | ||
| − | I | + | I tend to take a long view of things. I forge on medium chances. I am able to ignore the pain of a failed forging, because I know that I'm saving precious Radiants overall. |
| − | I have | + | Over the years I and others have given this advice in many threads on the ''Spiral Knights'' forums. Routinely I encounter knights, who favor forging at 100% chances, because the pain of a failed forging is unacceptably unpleasant. These knights are risk-averse — maybe not at the 95% level, but somewhere beyond the 70% level. |
| − | Ultimately, each knight should pick the level of risk that she can tolerate. This guide exists, just to help you understand the compromises that you're making. In particular, if you tend to forge at 100% chances, then please know that | + | Ultimately, each knight should pick the level of risk that she can tolerate. This guide exists, just to help you understand the compromises that you're making. In particular, if you tend to forge at 100% chances, then please know that you could lower your Radiant costs by approximately 10% by accepting slightly more risk. |
Latest revision as of 12:24, 18 August 2018
This article explains why Spiral Knights should consider forging 5-star items with medium (70%-80%) chances rather than 100% chances. It describes theory and experiment that you can interpret to make the best decision for your level of comfort with risk.
Contents
Assumptions
We ignore forge bonuses entirely. Double level-ups are highly relevant, but they do not appear to be affected by forging chances. Prize boxes are very rare. A 25% heat bonus is not relevant.
We assume that the forging tries are independent of one another and that the chances are as stated. Data sets collected by players do not offer any statistically valid evidence that the chances are otherwise.
We also assume that the knight never gives up, no matter how bad her luck is.
Theory
When a knight uses 100% forging chances, heating one 5-star item always costs 453 Radiant Fire Crystals. When a knight uses medium chances, the cost of heating a 5-star item varies.
The minimum cost is a mere 302 Radiants. This cost is achieved when all nine forgings from heat level 1 to heat level 10 succeed on their first tries. The probability is
- (0.80)3 * (0.75)3 * (0.70)3 = 7.4%.
So 92.6% of the time the cost will be greater than 302.
Basic probability theory lets us compute the expected cost, which you can think of as the cost incurred by a knight experiencing average luck. We expect to try 1 / p times to complete a task, if each trial has probability p of success. For example, forging from heat level 1 to heat level 2 has p = 0.80, so we expect 1 / 0.80 = 1.2 forgings and an expected cost of 1.2 * 6 = 7.2 Radiants.
If we add up the expected costs for all nine forgings, then we find that the expected total cost is around 419 Radiants. That is, a knight experiencing average luck will spend 419 Radiants.
Some knights will experience better-than-average luck and spend fewer than 419 Radiants, down to the minimum of 302. Some knights will experience worse-than-average luck and spend more than 419 Radiants. In fact, there is no theoretical maximum. A very unlucky knight might spend more than 1,000 Radiants.
Experiment
To get a more detailed picture of the possible costs for medium chances, we perform a computer simulation. Working in Python 3.x, we use a random number generator to compute 1,000,000 simulations of knights forging 5-star items from heat level 1 to heat level 10. For each of the 1,000,000 simulations, we record how many Radiants were required.
In accordance with the theory, the average is 419.447. The minimum of 302 is achieved in about 7.4% of the simulations. The maximum is 1,258.
In the plot, the horizontal axis shows the number of Radiants used, from 302 to 1,258. The vertical axis shows how many of the 1,000,000 simulations used that number of Radiants.
The median number of Radiants used is 400. The average is greater than the median, because a few simulated knights incurred big costs that pulled up the average. These simulations fill the "long tail" on the right side of the plot.
For our later analysis, it is useful to identify five "bins" of simulation results.
- 7% used 302 Radiants.
- 43% used between 303 and 400.
- 20% used between 400 and 452.
- 25% used between 454 and 597.
- 5% used 597 or more.
Analysis
When forging with medium chances, the only guarantee is that you will spend at least 302 Radiants. You risk spending more than that. But probability theory helps you manage that risk.
Some knights are highly risk-averse, so they wonder, "How bad could the cost be?" And the answer is, "There is no limit to how bad it can be." But this attitude is overly pessimistic. A person who is unwilling to accept any risk cannot ride in an automobile, cross a street, walk in a crowd, or do much of anything in life.
A reasonable pessimist asks, "How high would the cost be, if my luck were worse than 95% of other knights?" And the answer is around 597. So that kind of knight should forge at 100% chances and accept the 453-Radiant cost. But keep in mind that using 302 Radiants is more probable than using 597 or more.
A milder pessimist might ask, "How high would the cost be, if my luck were worse than 70% of other knights?" And the answer is around 453. So it makes little difference whether that knight forges at 100% chances or medium chances.
However, the best assumption is arguably that you will experience average luck. Then forging costs you somewhere around 419 (average) or 400 (median) Radiants. So you should forge with medium chances and save 34-53 Radiants per item.
The assumption of average luck is especially appropriate for knights who heat many items over a long time period. Even if these knights start off lucky or unlucky, their cumulative luck tends to approach the average as they heat more and more. This phenomenon is called regression toward the mean.
Knights who are on Cradle for a short time and heat only a few 5-star items are more probable (but still not highly probable) to experience extremes of good or bad luck. For them, adopting a pessimistic attitude to avoid the worst-case scenario makes slightly more sense.
Advice
I tend to take a long view of things. I forge on medium chances. I am able to ignore the pain of a failed forging, because I know that I'm saving precious Radiants overall.
Over the years I and others have given this advice in many threads on the Spiral Knights forums. Routinely I encounter knights, who favor forging at 100% chances, because the pain of a failed forging is unacceptably unpleasant. These knights are risk-averse — maybe not at the 95% level, but somewhere beyond the 70% level.
Ultimately, each knight should pick the level of risk that she can tolerate. This guide exists, just to help you understand the compromises that you're making. In particular, if you tend to forge at 100% chances, then please know that you could lower your Radiant costs by approximately 10% by accepting slightly more risk.