User:Jdavis/Forging
From SpiralKnights
This article explains why Spiral Knights players should consider forging 5-star items on medium (70%-80%) chances rather than 100% chances.
Theory
This section ignores forge bonuses such as prize boxes (which are rare) and double level-ups (which do not appear to be affected by forging chances). We assume that they do not happen.
When a knight uses 100% forging chances, heating one 5-star item costs a total of 453 Radiant Fire Crystals.
When a knight uses medium chances, the total cost of heating a 5-star item varies. The minimum cost, achieved when all forgings succeed, is a mere 302 Radiants. But usually the cost is greater than that.
We can use basic probability theory to compute the expected cost, which one can think of as the cost incurred by a knight experiencing average luck. We assume that the tries are independent of one another and that the chances are as stated. (Data sets collected by players do not offer any statistically valid evidence that the chances are otherwise.) We also assume that the knight never gives up, no matter how bad her luck is.
The key fact from probability is that we expect to need 1 / p trials to complete a task, if each one has probability p of success. For example, forging from heat level 1 to heat level 2 has p = 0.80 and so we expect 1 / 0.80 = 1.2 forgings to succeed, for an expected cost of 1.2 * 6 = 7.2 Radiants.\
If we add up the expected costs for all nine forgings from heat level 1 to heat level 10, then we find that the expected total cost is around 419 Radiants. That is, a knight experiencing average luck will spend around 419 Radiants.
Some knights will experience better-than-average luck and spend fewer than 419 Radiants, down to the minimum of 302. Some knights will experience worse-than-average luck and spend more than 419 Radiants. In fact, there is no theoretical maximum. A very unlucky knight might spend more than 1,000 Radiants.
Experiment
To get a more detailed picture of the possibile costs, we perform a computer simulation. Working in Python 3.x, we use a random number generator to compute 1,000,000 simulations of knights forging 5-star items from heat level 1 to heat level 10. For each of the 1,000,000 simulations, we record how many Radiants were required.
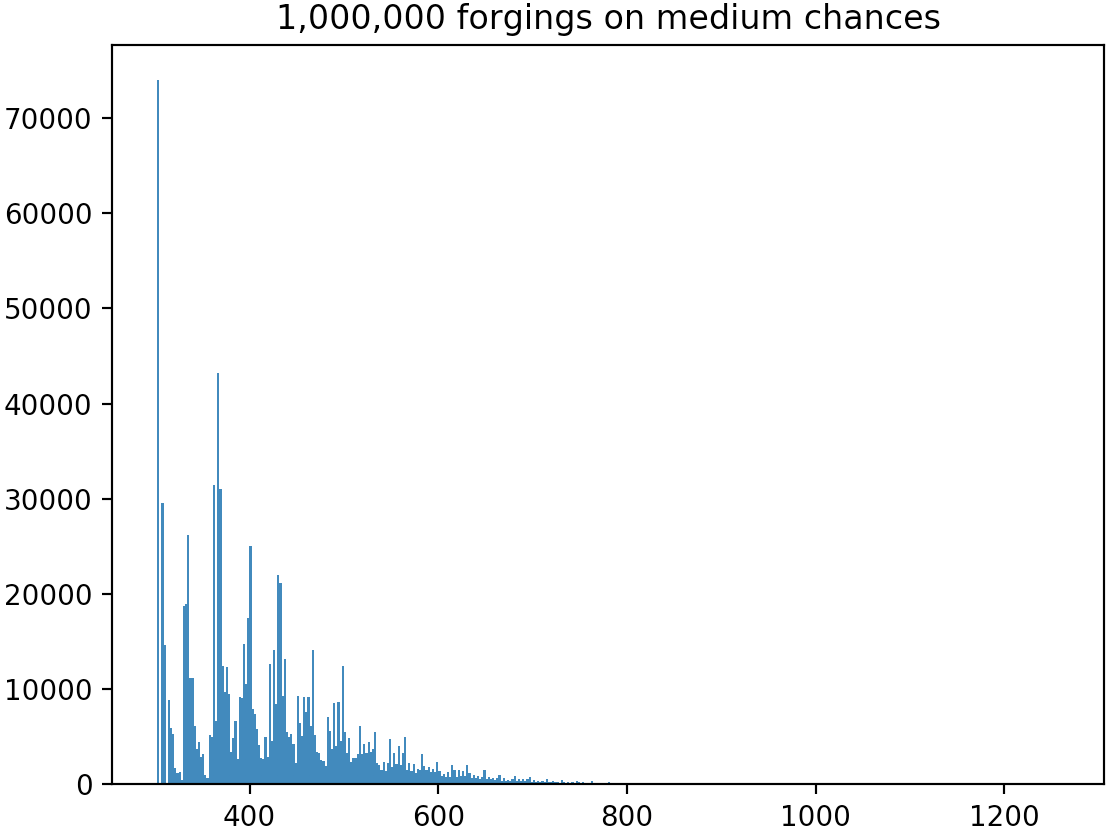
In accordance with the theory, the minimum number of Radiants was 302 and the average was 419.447. The maximum was 1,258.
In the plot, the horizontal axis shows the number of Radiants used, from 302 to 1,258. The vertical axis shows how many of the 1,000,000 simulations used that number of Radiants. 557,324 of the simulations used fewer than 419 Radiants. 139,708 of the simulations used between 419 and 453 Radiants. 302,968 of the simulations used more than 453 Radiants.
In other words, about 70% of the simulations used fewer than the 453 Radiants required for 100% chances, and 30% used more than 453 Radiants. Even after taking the unlucky latter group into account, forging on medium chances saved an average of about 34 Radiants over forging on 100% chances.
Advice
This section is unfinished.
Some players are risk averse. The 95% threshold is above 453.
Some players play for a short amount of time. Their luck might be far from average --- either good or bad.
But players who play for a long time, forging many items, will tend to have luck that is very close to average. And players with average luck should forge on medium chances to save some Radiants.